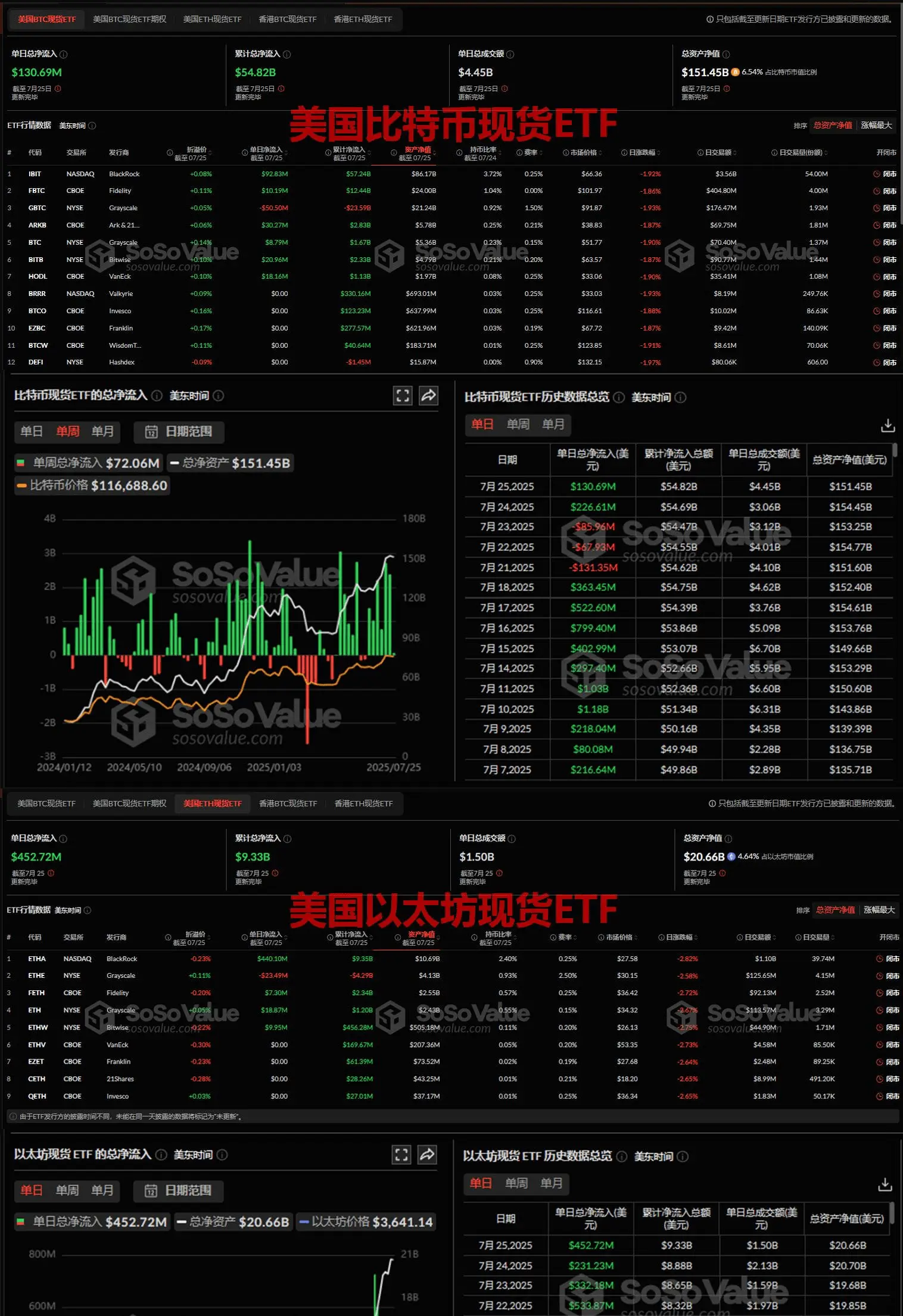
回顾历史,我们不难发现资产价格的长期走势往往超出人们的想象。以美国房地产为例,从20世纪70年代的3万美元到如今的60万美元,房价增长了20倍。这种涨幅在当时可能被认为是不可思议的,但事实证明,长期来看,具有内在价值的资产往往会随着时间的推移而升值。
这一现象同样适用于比特币。从数学的角度来看,比特币的价值走向只有两种可能:要么归零,要么持续增长。虽然归零的可能性始终存在,但只要比特币不归零,其价值就很可能会持续上涨。
让我们用一个简单的数学模型来解释这一点。假设比特币的价值是一个常数函数f(t)=c1,而法定货币的价值是一个指数衰减函数g(t)=c2e^(-at)。这里的a代表通货膨胀率,按照凯恩斯的理论,温和通胀率约为2%。因此,当我们用法定货币来衡量比特币的价值时,我们会发现比特币的相对价值呈指数增长。
这个模型虽然简化了现实情况,但它揭示了一个重要的经济学原理:在一个通货膨胀的世界里,稀缺资产的相对价值往往会上升。比特币作为一种新型的去中心化数字资产,其稀缺性和全球性使其具有独特的价值存储功能。
然而,比特币的价值不仅仅取决于数学模型,还需要社会共识的支持。越来越多的人认识到并相信比特币的价值,这种信念本身就成为了比特币价值的一部分。从这个角度来看,比特币确实具有某些类似于宗教或超国家机构的特征,但它的开放性、透明度和自由参与的特性使其优于传统的价值存储方式。
最后,我们需
这一现象同样适用于比特币。从数学的角度来看,比特币的价值走向只有两种可能:要么归零,要么持续增长。虽然归零的可能性始终存在,但只要比特币不归零,其价值就很可能会持续上涨。
让我们用一个简单的数学模型来解释这一点。假设比特币的价值是一个常数函数f(t)=c1,而法定货币的价值是一个指数衰减函数g(t)=c2e^(-at)。这里的a代表通货膨胀率,按照凯恩斯的理论,温和通胀率约为2%。因此,当我们用法定货币来衡量比特币的价值时,我们会发现比特币的相对价值呈指数增长。
这个模型虽然简化了现实情况,但它揭示了一个重要的经济学原理:在一个通货膨胀的世界里,稀缺资产的相对价值往往会上升。比特币作为一种新型的去中心化数字资产,其稀缺性和全球性使其具有独特的价值存储功能。
然而,比特币的价值不仅仅取决于数学模型,还需要社会共识的支持。越来越多的人认识到并相信比特币的价值,这种信念本身就成为了比特币价值的一部分。从这个角度来看,比特币确实具有某些类似于宗教或超国家机构的特征,但它的开放性、透明度和自由参与的特性使其优于传统的价值存储方式。
最后,我们需
BTC2.14%